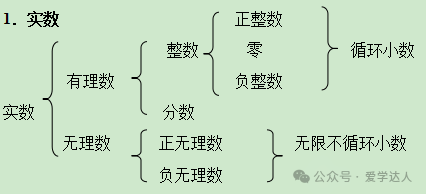
差比法,即:如果a - b > 0 , 那么 a > b ; 如果a - b =0 , 那么 a = b ; 如果a - b < 0 , 那么a < b .
解一元一次方程的步骤:去分母、去括号、移项、合并同类项、把未知数的系数化为1, 最终把一元一次方程变形为x=b 的形式
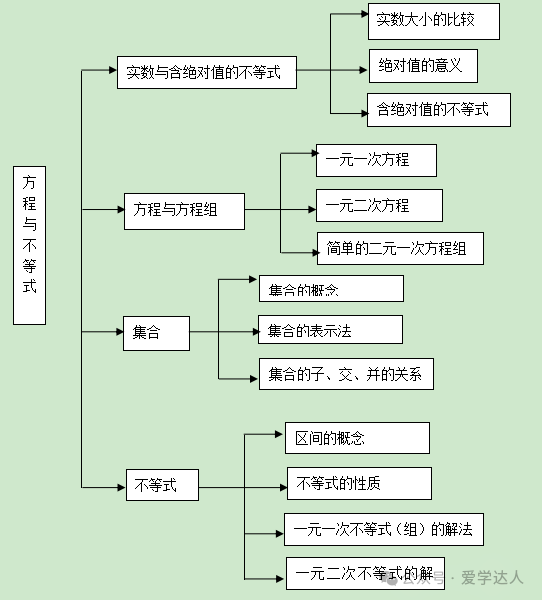
因式分解方法有:提取公因式法,公式法(平方差、完全平方、立方和、立方差等)、十字相乘法(关键:拆两边,凑中间,因式横向写)1.集合:自然数集N.整数集Z.正整数集Z+或N+.有理数集Q.实数集R.空集Ø,{0}表示含有一个元素“0”的集合,是不含任何元素的集合空集与任何集合的交集仍为空集,空集与任意集合A的并集仍为集合A(2)描述法:{代表元素|元素所具有的特征性质}.(2).集合与集合之间的关系:包含关系:子集:A⊆B则集合A是集合B的子集.注:任何集合是它自身的子集;空集是任何集合的子集。1、区间表示:各种区间表示的集合列表如下(表中a、b为任意实数,且a<b)

一元一次不等式的求解:去分母、去括号、移项、合并同类项、化未知数的系数为1(注意不等式性质应用)一元一次不等式组的求解:先求出不等式组中各个不等式的解集,然后再求出这些解集的交集,即是原不等式组的解集一元二次不等式解法: 将一元二次不等式左边因式分解,利用一次不等式组的解法,即可求出解集;当一元二次不等式左边的二次三项式不能分解时,可通过配方法将该二次三项式转化为含有完全平方式的形式,并加以讨论来决定不等式的解集